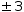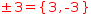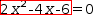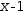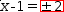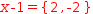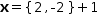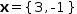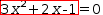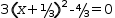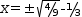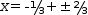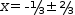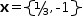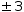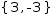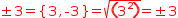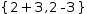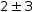6.1 Roots and Sets
When simplified or evaluated, a subexpression like  √9
is transformed to a positive number if the root is an integer
but note that information
is lost because the negative root is discarded.
If it is necessary to retain both roots, special simplification of
√9
is transformed to a positive number if the root is an integer
but note that information
is lost because the negative root is discarded.
If it is necessary to retain both roots, special simplification of
 √9 transforms to
√9 transforms to 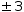 ±3.
But it is important to realize that the plus-or-minus unary operator
really evaluates to two values (unless the operand is zero). To work with
expressions like this, the distribution of
unary ± produces a set with two elements. That is,
±3.
But it is important to realize that the plus-or-minus unary operator
really evaluates to two values (unless the operand is zero). To work with
expressions like this, the distribution of
unary ± produces a set with two elements. That is,
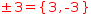 .[±3={3, -3}].
.[±3={3, -3}].
Note this will very likely change the type of the expression in which it appears.
A real example of this happens when complete-the-square (§3.4.10) is applied to
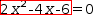 .{2⋅x^2-4⋅x-6}=0.
.{2⋅x^2-4⋅x-6}=0.
After simplifying and isolating
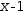 x-1
x-1, the equation appears
as
 x-1=±2
x-1=±2. This is where a set is introduced. Distributing
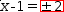 x-1=.{±2}
x-1=.{±2}
produces
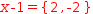 .[x-1={2, -2}]
.[x-1={2, -2}]
(note this expression is invalid because it is unbalanced with respect to type).
After isolating x, the expression becomes
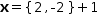 xʂ={2, -2}+1
xʂ={2, -2}+1
and simplifying again produces
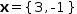 xʂ={3, -1}
xʂ={3, -1}.
Binary ± operates in a similar way. An example is this: completing the square
of
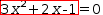 .{3⋅x^2+2⋅x-1}=0
leads to
.{3⋅x^2+2⋅x-1}=0
leads to
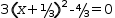 3⋅(x+1/3)^2-4/3=0; isolating x gives
3⋅(x+1/3)^2-4/3=0; isolating x gives 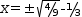 x=±(√(4/9))-1/3.
Now, commute the the term with the radical to the right and distribute the radical:
x=±(√(4/9))-1/3.
Now, commute the the term with the radical to the right and distribute the radical:
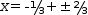 x=-(1/3)+±(2/3)
(here, ± is a unary operator); and simplify again:
x=-(1/3)+±(2/3)
(here, ± is a unary operator); and simplify again:
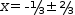 x=-(1/3)±2/3
(here, ± is a binary operator). Distribute the binary ± and simplify
to give the roots
x=-(1/3)±2/3
(here, ± is a binary operator). Distribute the binary ± and simplify
to give the roots
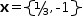 xʂ={1/3, -1}.
xʂ={1/3, -1}.
Working with unary and binary ± leads to non-scalar intermediate results that
can lead, in turn, back to scalar expressions. The remainder of this section
explores this idea.
Distributing unary ± produces a set in which the operand of ± appears
twice, once negated:
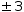 ±3 Distribute is
±3 Distribute is
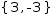 {3, -3}.
{3, -3}.
Applying Factor to a set consisting of two elements, one of which is the
negation of the other, produces a unary ± whose operand is the square
root of the positive set element, squared.
Distribute, factor and simplify provide a three-cornered cycle for
unary ±. Try this: enter the four-part equivalence
 ±3=±3=±3=±3. Distribute the second part; distribute and factor the third part;
for the fourth part, distribute and factor it, then evaluate its radical. You will end up
with the following equivalence:
±3=±3=±3=±3. Distribute the second part; distribute and factor the third part;
for the fourth part, distribute and factor it, then evaluate its radical. You will end up
with the following equivalence:
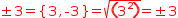 .[±3={3, -3}=√(3^2)=±3].
.[±3={3, -3}=√(3^2)=±3].
Distributing binary ± produces a set in which the left operand is
combined with the right operand, once using addition and once using
subtraction:
 .{2±3} Distribute is
.{2±3} Distribute is
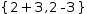 {2+3, 2-3}.
{2+3, 2-3}.
Factoring a set consisting of two elements, one of which is an
addition and the other a subtraction with matching corresponding
operands, produces a binary ± whose operands are those of either of
the elements. That is,
 .{{2+3, 2-3}} Factor is
.{{2+3, 2-3}} Factor is
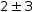 2±3.
2±3.